PROBLEMA DE JUNIO (Atención: las respuestas debes de entregarlas antes del 17 de Junio)
3º y 4º DE ESO:
Un señor se quiere comprar unas gafas de sol. Entra por la mañana a la tienda y, cuando se dirige al estante donde están las gafas de sol advierte que el cajero no está presente en ese momento. Más aún: el señor ve que hay un billete de 50 € sobre el mostrador, al lado de la caja. Mira a ambos lados y como no ve a nadie, coge el billete de 50 euros, deja las gafas y se va.
¡Robó el billete de 50 €!
Por la tarde, vuelve a la misma tienda. Ahora sí, hay un empleado en la caja. El señor se dirige al mismo estante, elige unas gafas y se fija en el precio: ¡30 €! Coge las gafas y se dirige a la caja. Aprovecha el billete de 50 € que robó por la mañana y paga. El cajero le devuelve 20 €. El señor se va de la tienda con paso ligero, las gafas y la vuelta.
¿Cuánto dinero perdió el negocio?
a) 20 €
b) 30 €
c) 50 €
d) 70 €
e) 80 €
f) 100 €
Tienes que razonar la respuesta.
BACHILLERATO:
Alba y Blanca se acaban de hacer amigas de Carlos, y quieren saber cuando es su cumpleaños. Carlos les da una lista con 10 posibles fechas:
15 de mayo 16 de mayo 19 de mayo
17 de junio 18 de junio
14 de julio 16 de julio
14 de agosto 15 de agosto 17 de agosto
Carlos les dice a Alba y Blanca por separado el mes y el día de su cumpleaños respectivamente.
– Alba: No se cuando es el cumpleaños de Carlos, pero sé que Blanca tampoco lo sabe.
– Blanca: Al principio no sabía cuando era el cumpleaños de Carlos, pero ahora lo sé.
– Alba: Entonces yo también sé cuando es el cumpleaños de Carlos.
Así qué, ¿podrías decir cuándo es el cumpleaños de Carlos?
PROBLEMA DE MAYO
3º DE ESO:
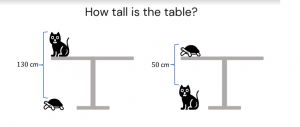
4º DE ESO:
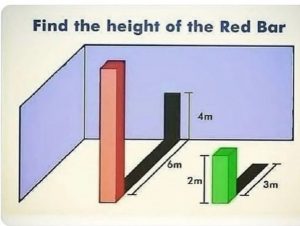
BACHILLERATO:

PROBLEMA DE ABRIL
3º DE ESO
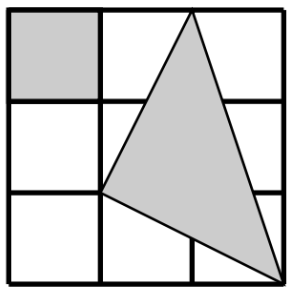
Calcula razonadamente el área del triángulo gris sabiendo que el área del cuadrado sombreado son 4 cm².
4º DE ESO
Miguel Ángel ha repartido un bizcocho entre sus tres amigos. En principio, dio a Julia 2/3 del total; a Marta 1/5 del total; y lo que sobró se lo dio a Hugo. Al instante, Marta protestó, y Julia le dijo «anda, toma un cuarto de mi parte». Hugo quedó triste y Julia le dio un quinto de lo que ahora tenía. Si después de la última negociación el trozo de Hugo pesa 140 gramos, ¿cuántos gramos pesa la porción de Marta? ¿cuánto pesa el bizcocho entero?
BACHILLERATO:
Marta, Paola y Julen van a comprase tres gorras, una para cada uno. En la tienda sólo tienen 5 gorras: dos blancas y tres rojas. Los amigos no terminan de decidirse por qué gorra comprar, y el dependiente les propone el siguiente juego:
“Si les parece, ustedes cerrarán los ojos, yo les pondré una gorra a cada uno y esconderé las restantes. Después, cuando abran los ojos, si alguno de ustedes adivina el color de la gorra que lleva puesta, podrá llevársela sin pagar”.
Así lo hicieron. Después de abrir los ojos, se miraron unos a otros, pasaron unos minutos y Marta dijo:
“¡Ya está! Mi gorra es de color rojo”.
Demuestra que estaba en lo cierto.
PROBLEMA DE MARZO
3º DE ESO
Irene tiene dos mascotas muy juguetonas, el conejo Bigotes y su fiel perro Duque. Les encantan jugar al pilla-pilla. Una tarde Bigotes lleva una ventaja a Duque que lo persigue equivalente a 50 saltos del conejo. Si un salto de Duque equivale a tres saltos del conejo y el conejo da ocho saltos mientras el perro da tres, ¿en cuántos saltos alcanza Duque a su amigo Bigotes?
4º DE ESO
Durante el cumpleaños de Marta su amigo Hugo, que siempre está buscando problemas (de matemáticas), hace la siguiente observación sobre la tarta que están a punto de devorar:
«Si realizamos un corte recto a la tarta, obtenemos dos trozos. Con un segundo corte recto que cruce el anterior, conseguimos cuatro trozos y con un tercer corte recto podemos llegar a siete trozos de tarta».
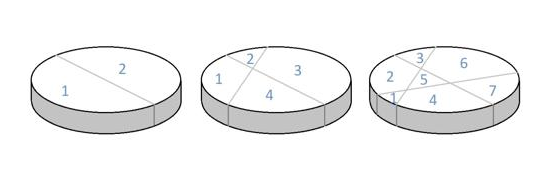
Hugo propone como reto encontrar el mayor número de trozos (no necesariamente iguales) que podemos conseguir con exactamente 7 cortes rectos.
BACHILLERATO:
Lourdes ha convencido a cuatro amigos para que vayan con ella a poder los olivos trabajando de lunes a viernes por las tardes.
Cada día, cuatro de ellos podaban y el otro les ayudaba. Cada uno de ellos podó el mismo número de árboles cada día, es decir Lourdes podó durante 4 días el mismo número de olivos, y así cada uno de sus amigos.
Los resultados de la poda fueron: lunes, 35 árboles podados; martes, 36; miércoles, 38; jueves, 39, y el viernes no sabemos si fueron 36 ó 38. Calcula cuántos árboles diarios podó cada uno, sabiendo que fueron números enteros y que ninguno podó los cinco días.
PROBLEMA DE FEBRERO
3º DE ESO
En una celebración por el final de trimestre, un grupo de amigos y amigas de 3º de ESO preparan una comida en en el pantano de Béznar. Cada dos comparten un plato de arroz, cada tres una tortilla de patatas, y cada cuatro, un plato de carne. Si en total se prepararon 65 platos:
a) ¿Cuántos amigos se reunieron?
b) ¿Cuántos platos de cada clase se prepararon?
4º DE ESO
La madre de Juan le ha encargado que apague el horno justo cuando pasen 15 minutos para que el asado esté en su punto. Pero Juan, tan solo dispone de dos relojes de arena, uno mide 11 minutos y el otro 7 minutos. ¿Cómo puede cronometrar exactamente los 15 minutos que le pide su madre?
BACHILLERATO
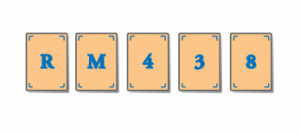
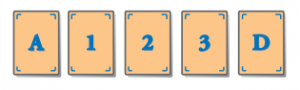
Andrés y Belén están jugando con una baraja de cartas algo peculiar, cada carta tiene por una cara una letra y por la otra un número natural.
Andrés afirma que «cualquier carta que tenga en un lado una vocal, tiene un número par en el otro lado». Entonces coloca 5 cartas sobre la mesa:
¿A qué cartas debe de dar la vuelta Belén para convencerse de que Andrés dice la verdad?
Si Andrés hubiera sacado las siguientes cartas, ¿cuáles tendría que levantar Belén para saber que la afirmación de Andrés es cierta?
PROBLEMA DE ENERO
3º DE ESO
Al campeonato de ping-pong organizado en el instituto se han apuntado 128 alumnos y alumnas de todos los cursos. El torneo se juega por simple eliminación, es decir, el jugador que pierde un partido queda eliminado. ¿Cuántos partidos se jugaran en total para definir al ganador?
4º DE ESO
En una excursión a la cruz de Nigüelas, organizada por el profe de educación física, cada tres alumnos/as comparten una mochila; cada cuatro, una brújula, y cada seis, un mapa de la zona. Si entre mochilas, brújulas y mapas hay 27 objetos. ¿Cuántos alumnos/as participan en la excursión?
BACHILLERATO
Antonio tiene un cortijo de planta rectangular de 10 m x 20 m. En una de las esquinas deja atada a su querida cabra con una cuerda de 30 m de longitud para que pueda pastar la hierba que hay alrededor del cortijo. Dibuja un esquema con la porción de parcela en la que puede pastar la cabra y calcula su superficie.
PROBLEMA DE DICIEMBRE
3º DE ESO
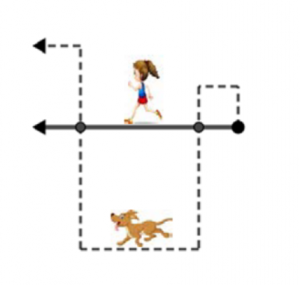
Como todas las mañanas Marina sale a correr 12 km acompañada de su perrito Duque. Marina lo hace en línea recta, pero Duque va y viene formando cuadrados alrededor de la trayectoria de Marina y cruzándose con ella de vez en cuando, como ves en la figura, hasta coincidir con ella al final de la trayectoria. Ya sabemos que Marina recorre 12 km, pero: ¿Cuántos kilómetros corre Duque?
4º DE ESO
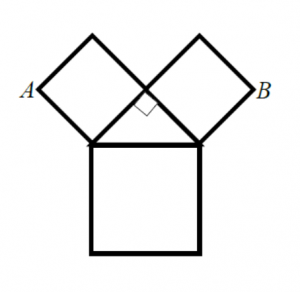
En la plaza de la iglesia de Tablate hemos encontrado una curiosa figura marcada en el suelo. Está formada por un triángulo rectángulo isósceles y tres cuadrados. Si la distancia entre A y B son 12 cm, ¿Cuál es el área, en cm2, de toda la figura?
BACHILLERATO:
Siete amigos están sentados alrededor de un fuego pasando una velada en el campo. Se numeran del 1 al 7. Otro amigo, Juan, está de pie y realizan el siguiente juego:
Juan se pone a dar vueltas al círculo tocando a sus amigos en la espalda de forma alterna, empezando por el marcado como el número 1, a uno si al siguiente no. Al que toca se debe de levantar.
Al acabar la vuelta, comienza otra, de tal forma que si toca a un compañero que está sentado, este se debe de levantar, y si está de pie, se tiene que sentar.
- ¿Qué amigos están de pie al terminar la segunda vuelta?
- ¿Y al terminar la 3ª , 4ª y 5ª vuelta?
- Después de 2022 vueltas, ¿Quiénes estarán de pie?
PROBLEMA DE NOVIEMBRE
3º DE ESO
La figura siguiente es un cuadrado formado por dos azulejos cuadrados y tres rectangulares, unidos por el lado más largo.
Cada una de las piezas cuadradas tiene 72 centímetros de perímetro.
¿Cuál será el perímetro de las piezas rectangulares?

4º DE ESO
A partir de un cuadrado, encontramos los puntos medios de los lados y unimos cada vértice con uno de los puntos medios.
A partir de esas líneas, dibujamos el octógono amarillo que vemos en la figura.
Calcula la proporción del área total del cuadrado que ocupa ese octógono.
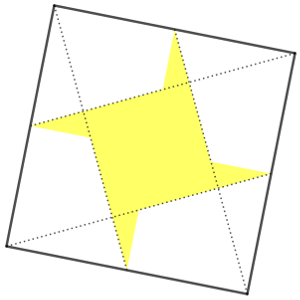
Ayuda: Intenta descomponer la figura amarilla en triángulos fáciles de manejar.
BACHILLERATO
Los municipios de Albuñuelas, Saleres, Melegís y Restábal deben comprar mascarillas de protección médica para el personal sanitario de sus centros de salud.
Con el objetivo de obtener un mejor precio, se ponen en contacto para hacer un pedido conjunto.
Han hablado con Ana, que es la funcionaria encargada de pedirlas, y por las anotaciones que ésta ha hecho, sabemos que entre Albuñuelas, Saleres y Melegís necesitan 148 cajas, pero entre Restábal, Saleres y Melegís necesitan 126. Además, entre Restábal, Albuñuelas y Melegís necesitan 140 cajas y entre Restábal, Saleres y Albuñuelas, 114.
¿Puedes averiguar cuántas cajas necesita en realidad cada municipio? ¿Y cuántas debe pedir en total?