El año 2018 empieza muy bien para las Matemáticas, y sobre todo para los números primos.
El día 3 de enero de 2018, el grupo GIMPS anunciaba el descubrimiento (y la confirmación) del mayor número primo conocido hasta la fecha. Este número primo tiene nada más y nada menos que 23249425 dígitos (¡23 millones!).
Como ya sabes, los números primos son aquellos que solo se pueden dividir por sí mismos y por la unidad, como 2, 3, 5, 7, 11, 13, 17… Están considerados los átomos de las matemáticas, sus ladrillos indivisibles, ya que cualquier número entero se puede descomponer como el producto de unos números primos.
Desde aproximadamente el año 300 A.C. y gracias a Euclides sabemos que el conjunto formado por los números primos es infinito, pero son muy difíciles de encontrar cuando avanzamos en los números naturales.
Para hacerse una idea de la magnitud de este gigantesco número primo podemos utilizar el siguiente símil:
Imaginad que escribís tremendamente rápido, digamos 3 dígitos por segundo. Buena velocidad, ¿verdad? Bien, pues con esa frecuencia de escritura, y sin parar en ningún momento, tardaríais casi 3 meses en escribirlo entero.
El número hallado pertenece a una familia especial de números primos, la de los primos de Mersenne. Responden a la forma 2^n – 1. Por ejemplo, 2^2 – 1 = 3, así que 3 es el primer primo de Mersenne.
En el año 1588, el matemático italiano Pietro Cataldi demostró que 2^17 – 1 = 131.071 es primo, el mayor primo de Mersenne hasta entonces. En todos estos siglos, la humanidad solo había encontrado 49 primos de esta familia. El detectado ahora es el quincuagésimo. Se obtiene con la fórmula 2^77.232.917 – 1 y tiene 23.249.425 cifras, casi un millón más que el anterior récord, obtenido hace dos años. A este número de Mersenne se le designa como:
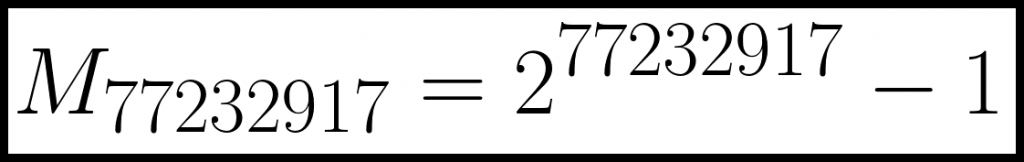
La búsqueda de estos primos gigantescos no es un mero pasatiempo. El algoritmo criptográfico RSA, que se utiliza para garantizar la seguridad del intercambio de información en la web, está basado en la descomposición de números enteros en números primos. Cuanto más grandes sean estos, más difícil será romper el código. Las transacciones comerciales por internet y la privacidad de las comunicaciones dependen de estos gigantescos números primos.




